你知道什麼是「有效利率」?
一、有效利率(Effective Interest Rate;EIR)之定義與特性
(一) 定義
一般通稱年利率(即名目利率),是借貸雙方在契約上所定義的利率,其利息可能每半年、每季(3個月)、或每月複利一次,因此,基於複利期間之不同,就會產生不同的有效利率(EIR)。換言之,有效利率是特定支付利息條件下的真正利率水準。
(二) 特性
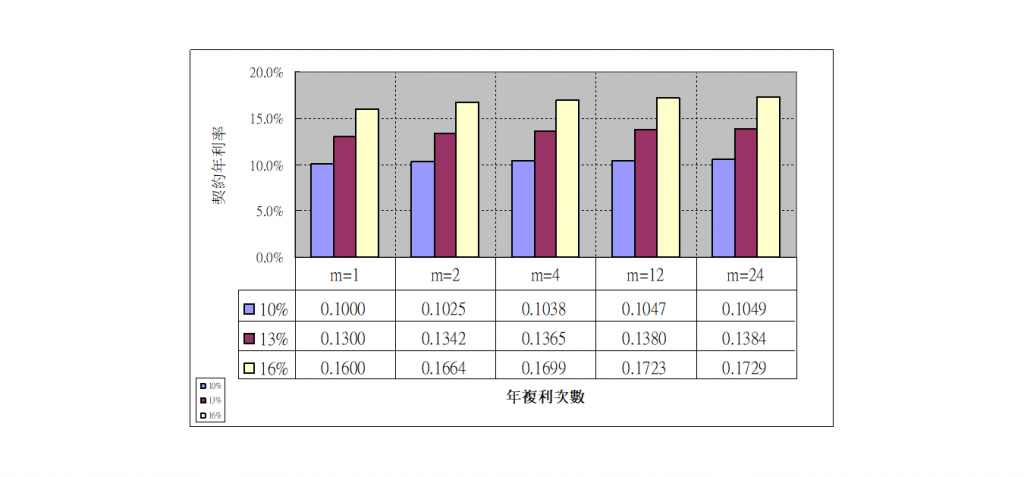
- 在同樣契約利率下,其複利單位時程愈短,複利次數愈多,有效利率會愈大。
- 在同樣複利次數下,契約利率愈高,有效利率漲幅會愈大。
二、有效年利率(Effective Annual Rate;EAR)之公式
(一) 公式
依據有效利率之觀念,假設借貸金額為一元,以一年為借貸之年期,其複率所產生之利息金額將等於一年單利(有效年利率)而所產生之利息金額,即:
(1+rt)=(1+ro/m)m×n
因為時間為一年,因此t=n=1 → (1+r)=(1+ro/m)m
→ EAR=r=(1+ro/m)m-1
其中 ro:表示每年複利m次之名目年利率
m:每年複利次數
(二) 計算範例
範例一:某銀行之牌告利率為9%,其每月複利一次,則有效年利率(EAR)為多少?
【解】
EAR=(1+ro/m)m-1 因為 ro=9% m=12
→ EAR=(1+9%/12)12-1=9.38%
範例二:某錢莊每借一萬元,月還利息五百元,請問有效年利率為多少?
【解】
每月利率為500/10000=5% 則 年利率=5%×12=60%
→ EAR=(1+60%/12)12-1=79.59%
版權所有 請勿盜用