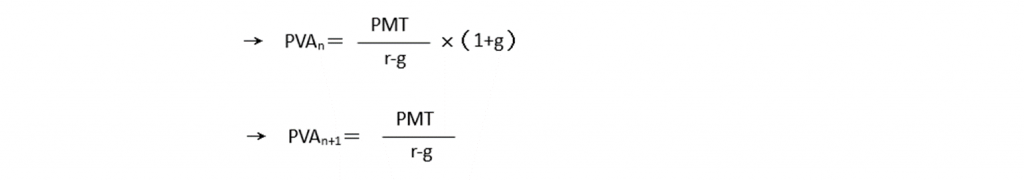成長型年金在不動產上之運用
一、成長型年金之公式
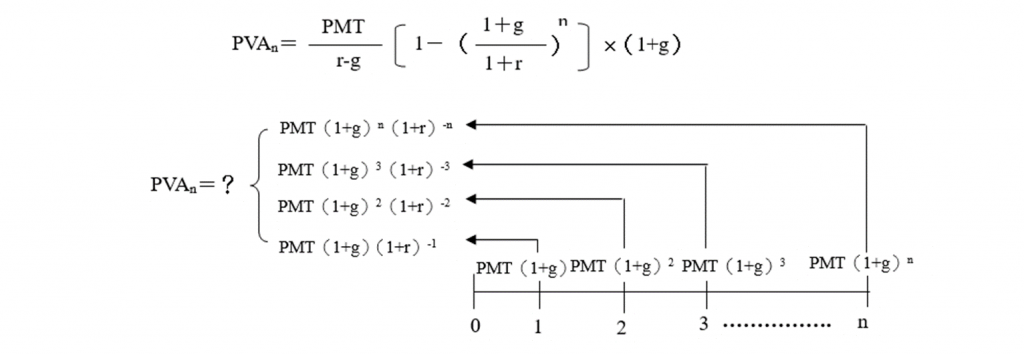
(一) 年金於第一年開始就以g之成長率每年增加
假設年金於第一就年開始就以g之成長率,每年增加,而n年後,以r之折現率折現,則:
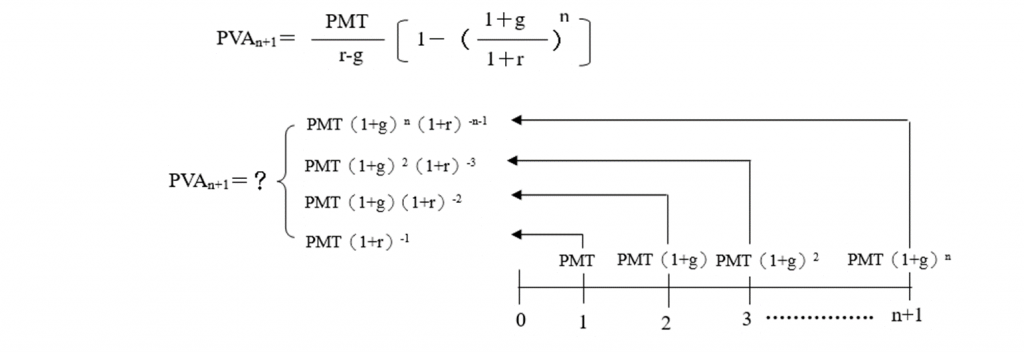
(二) 年金於第二年開始以g之成長率每年增加
假設年金於第二年開始以g之成長率,每年增加,而n+1年後(即成長n年後),以r之折現率折現,則:
(三) 公式討論
- 本公式亦稱為戈登模式(Gordon Model)
- 上式中g可為年金之成長率或是通貨膨脹率
- 如果 r>g並且n=∞
- 成長型永續年金現值公式成立的條件是r>g。反之,若g>r,則現金流量成長速度大於折現率,此將造成各期現金流量的現值不再是有限值。換句話說,未來的現金流量隨著時間愈久遠,對本期價值的影響愈強,此和一般現值概念相違背。一般現值概念應是未來現金流量的重要性會隨著時間愈久遠而變小。
二、成長型年金觀念在不動產上之運用
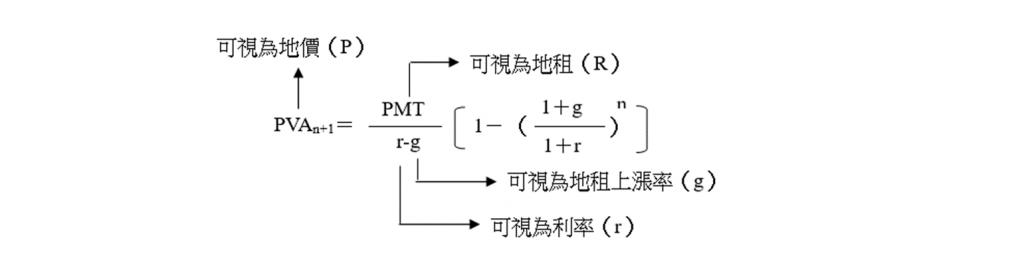
(一) 公式說明
(二) 公式討論
- 因為土地永遠不會毀滅而具有永續性,因此n=∞,如果利率 r>地租上漲率g,則P=R/(r-g)
- 如果地租上漲率g>利率 r →地價P=∞
此表示地價會無限上漲,若要防止此種情況發生,則有以下兩種措施:
(1) 提高融資放款利率,使得融資利率(r)>地租上漲率(g),因為利息高,地主就會賣土地,如此可增加土地的供給量,土地價格就不會上漲。
(2) 融資緊縮,也就是減少融資的放款額度,以減少土地之交易,而可避免地價之無限上漲。
版權所有 請勿盜用