財務數學中的單利與複利觀念 你清楚嗎?

一、單利（Simple Interest）之定義與公式

(一) 定義

所謂的單利係指貸款最終日之應付利息，只是基於原始本金而計算利息，而貸款期間所賺得之利息並不再孶生利息。

 

(二) 公式

PV＝FV_t（1+rt）^-1

其中  PV：現值或本金

FV_t：終值或t年後本利和

r：利率（通常為年利率）

t：每期的時間（通常以年計算）

（1+rt）^-1稱為單利的現值利率因子 (Prevent Value Interest Factor；PVIF)

 

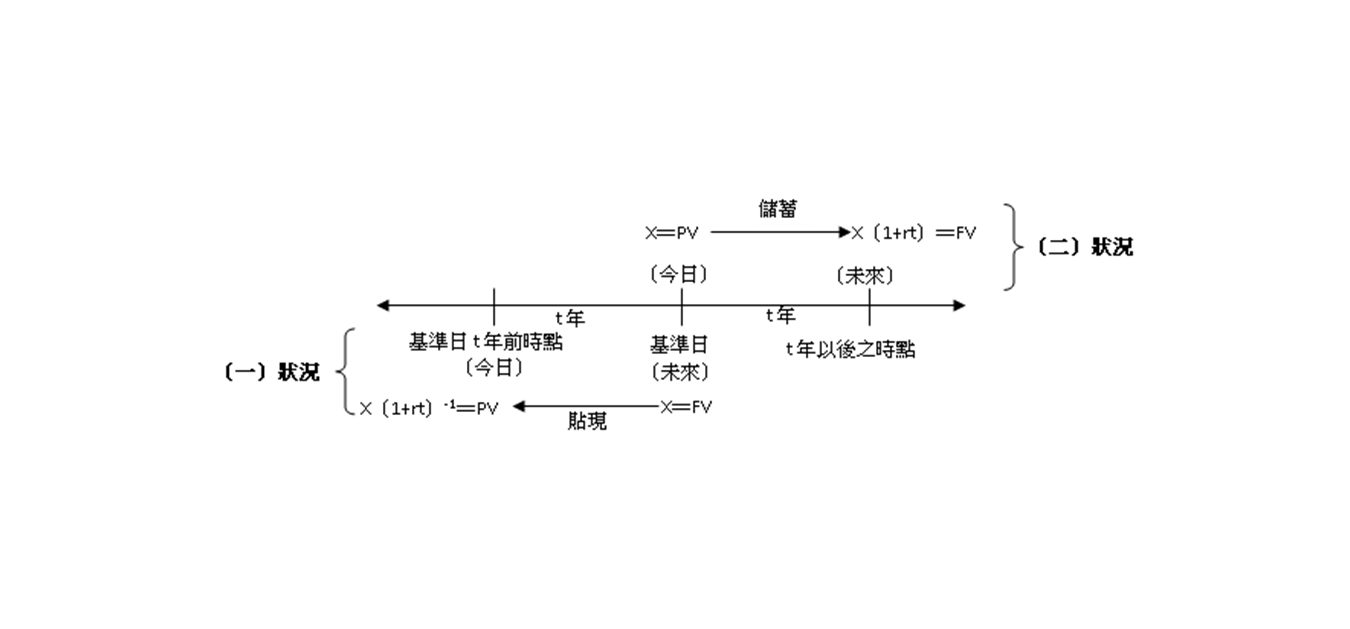
(三) 現值與終值之關係圖

1. 假設基準日t年前時點為今日，而基準日金額設為X，則基準日t年前（今日）現金應為X（1+rt）^-1之金額。（基準日為終值，今日為現值）

2.假設基準日為今日，並且金額設為X，則基準日t年以後金額應為X（1+rt）。（基準日為現值，t年後為終值）

二、複利（Compounding Interest）之定義與公式

(一) 定義

所謂的複利係指本金及任何已賺得但尚未支付或提取之利息來計算下一期之利息。換言之，本金所產生的利息會加入本金繼續在衍生利息，產生利上滾利的效果。

 

(二) 公式

PV＝FV_n（1+r）^-n＝FV_n×PVIF（i，n）  或

FV_n＝ PV（1+r）ⁿ＝PV×FVIF（i，n）

其中  PV：現值或本金

FV_n：終值或t年後本利和

n：利息的期數

r：每期利率

 

(三) 說明

1.（1+r）^-n稱為複利的現值利率因子（Prevent Value Interest Factor；PVIF），或稱為現值因子 (Prevent Value Factor；PVF)、一次支付現值因子（Single-Payment Present-Worth Factor；PW） 或稱為複利現價率（Prevent worth of one）。其意義為n年後的一元，折算為現值，為多少元。

2.（1+r）ⁿ稱為終值利率因子(Future Value Interest Factor；FVIF)，或稱為終值利率因子(Future Value Interest Factor；FVIF)、一次支付複利因子（Single-Payment Compound-Amount Factor；CA）、複利終價率（Amount of one）。其意義為現在存入一元，若以複利計算，n年後本利合計額為多少元。

3. 因為複利方式有多種，包括每年複利、每季複利及每月複利等，然若要利率（r）統一以年利率表示時，則上述之公式可改以下式表示：

FV_n＝ PV（1+r_m/m）^m×n

其中  r_m：年利率

m：每年複利次數

n：年數

請詳見以下Excel檔並可自行操作觀其變化。

不同複利方式FVIF

 

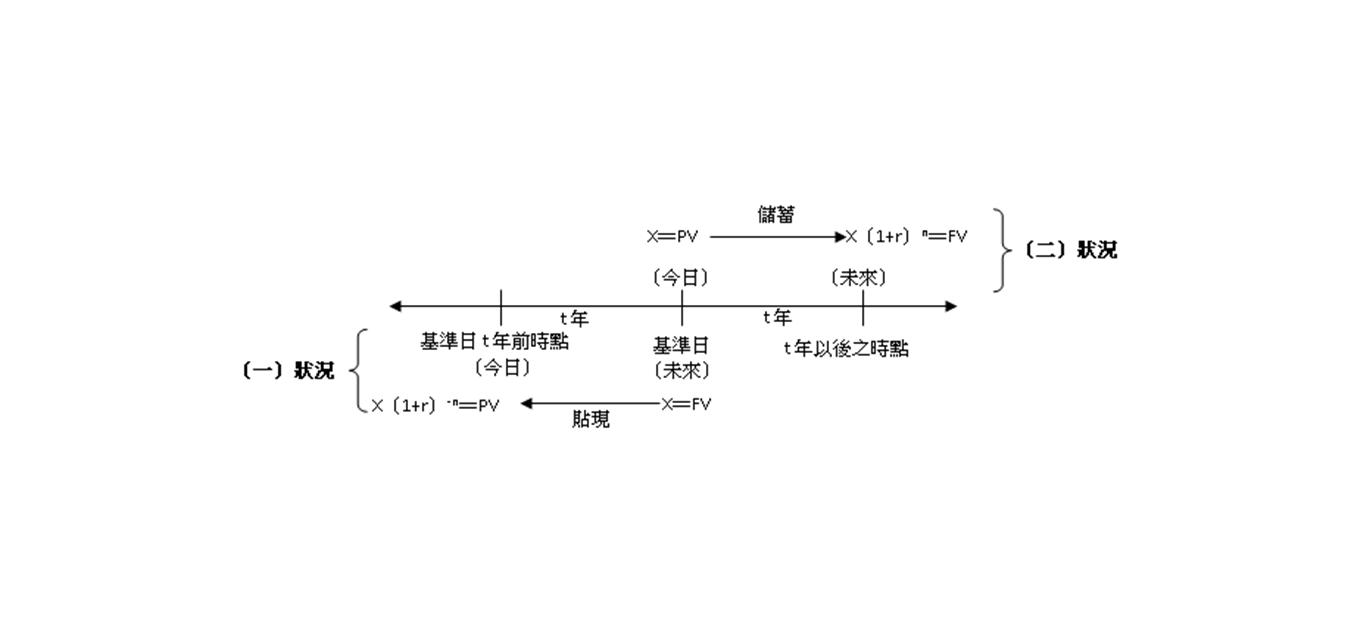
(四) 現值與終值之關係圖

1. 假設基準日t年前時點為今日，而基準日金額設為X，則基準日t年前（今日）現金應為（1+r）^-n之金額。（基準日為終值，今日為現值）
2. 假設基準日為今日，並且金額設為X，則基準日t年以後金額應為X（1+r）ⁿ。（基準日為現值，t年後為終值）

三、單率與複率利率因子比較分析

單率與複率現值利率因子比較及單率與複率終值利率因子比較，請詳見以下Excel檔並可自行操作觀其變化。

單率與複率利率因子比較

 

版權所有 請勿盜用